Парадокс растущего носа Пиноккио
Известная философская проблема известна как парадокс лжеца. По форме он выглядит очень просто: “Я лгу”. Пиноккио в этом случае говорит: “Мой нос сейчас растет”. Противоречие очевидно: нос мальчика растет только тогда, когда он говорит неправду, но в этом случае его утверждение о росте носа не должно быть верным. В то же время если деревянное дитя папы Карло лжет, то нос должен именно расти – так он устроен. Но тогда он не может утверждать, что нос растет – и так далее до бесконечности.
С точки зрения логики в классическом понимании эта проблема считается неразрешимой, поэтому утверждение “Я лгу” выходит за рамки логики вообще. Пусть другие мучаются.
Проблема настоящего времени
Чтобы что-то могло физически существовать, оно должно присутствовать в нашем мире в течение какого-то времени. Не может быть объекта без длины, ширины и высоты, а также не может быть объекта без «продолжительности» — «мгновенный» объект, то есть тот, который не существует хотя бы какого-то количества времени, не существует вообще.
Согласно универсальному нигилизму, прошлое и будущее не занимают времени в настоящем. Кроме того, невозможно количественно определить длительность, которую мы называем «настоящим временем»: любое количество времени, которое вы назовёте «настоящим временем», можно разделить на части — прошлое, настоящее и будущее.
Если настоящее длится, допустим, секунду, то эту секунду можно разделить на три части: первая часть будет прошлым, вторая — настоящим, третья — будущим. Треть секунды, которую мы теперь называем настоящим, можно тоже разделить на три части. Наверняка идею вы уже поняли — так можно продолжать бесконечно.
Таким образом, настоящего на самом деле не существует, потому что оно не продолжается во времени. Универсальный нигилизм использует этот аргумент, чтобы доказать, что не существует вообще ничего.
Парадокс Пето
Очевидно, что киты гораздо крупнее нас, это означает, что у них в телах гораздо больше клеток. А каждая клетка в организме теоретически может стать злокачественной. Следовательно, у китов гораздо больше шансов заболеть раком, чем у людей, так?
Не так. Парадокс Пето, названный в честь оксфордского профессора Ричарда Пето, утверждает, что корреляции между размером животного и раком не существует. У людей и китов шанс заболеть раком примерно одинаков, а вот некоторые породы крошечных мышей имеют гораздо больше шансов.
Некоторые биологи полагают, что отсутствие корреляции в парадоксе Пето можно объяснить тем, что более крупные животные лучше сопротивляются опухоли: механизм работает таким образом, чтобы предотвратить мутацию клеток в процессе деления.
Парадокс ценности, названный в честь Адама Смита
Этот феномен называется еще парадоксом воды и алмазов, он назван в честь автора трудов по теории экономики, Адама Смита. Считается, что он первым обнаружил и описал этот парадокс. В чем же он заключается?
Считается, что вода в качестве ресурса куда полезнее алмазов, хотя их цена в десятки и сотни раз выше. В общем-то, особо долго размышлять не придется – биологически и экономически вода действительно необходима человеку для поддержания качества своей жизни. В то же время без алмазов, по правде говоря, вполне можно прожить.
Кроме того, предельная полезность любого предмета падает при непрерывности его потребления – коротко говоря, если вы проведете несколько часов в раскаленной пустыне, стакан прохладной воды будет лично для вас дороже всех богатств мира. После утоления жажды вы спокойно потратите большее количество воды на то, чтобы умыть запыленное лицо, а дальше вы, возможно, захотите наполнить водой целое ведро, чтобы вымыть пол.
Старый новый корабль Тесея
Благодарные афиняне несколько столетий хранили корабль одного из своих отважных царей, Тесея. На нем было совершено путешествие в Афины с острова Крит. Судно от времени постоянно ветшало, постепенно некоторые его деревянные части заменялись новыми, чтобы корабль не разрушился. В результате через годы таких замен не осталось ни одного оригинального куска дерева. Можно ли теперь считать этот корабль именно тем, на котором путешествовал Тесей? Ни один из ответов на эту загадку нельзя признать стопроцентно верным, поскольку противоречия все равно остаются.
Между прочим, каждый из нас является в некотором роде таким кораблем: дело в том, что все клетки нашего организма полностью обновляются за семь лет. Означает ли это, что через означенное время в зеркале можно увидеть незнакомца? Или это все тот же старый добрый вы сам?
Парадокс всемогущего Бога
Способно ли всемогущее существо создать камень, который само окажется не в состоянии поднять? Если переводить в плоскость морали, вопрос будет звучать так: как в мире может существовать зло, если Бог является всемогущим? Ну и заодно – откуда тогда берется свобода воли и поступков отдельных людей, если Бог еще и всеведущ, а от судьбы не уйти?
Ответы на этот вопрос тоже парадоксальны по своей сути – аргументы одной из сторон становятся аргументами и другой стороны, только с обратным знаком. Если для одних этот парадокс является прямым доказательством отсутствия высших сил и, следовательно, поводом не верить в Бога, то для других именно этот парадокс доказывает, что Бог точно существует. Поэтому и допускает существование вообще всего – и зла в том числе, чтобы продемонстрировать свою силу и свою любовь к человеку.
Парадокс тритона
Соберите группу друзей и посмотрите все вместе это видео. Когда закончите, пусть каждый выскажет своё мнение, увеличивается звук или уменьшается во время всех четырёх тонов. Вы удивитесь, насколько разными будут ответы.
Чтобы понять этот парадокс, вам нужно знать кое-что о музыкальных нотах. У каждой ноты есть определённая высота, от которой зависит, высокий или низкий звук мы слышим. Нота следующей, более высокой октавы, звучит в два раза выше, чем нота предыдущей октавы. А каждую октаву можно разделить на два равных тритонных интервала.
На видео тритон разделяет каждую пару звуков. В каждой паре один звук представляет собой смесь одинаковых нот из разных октав — например, сочетание двух нот до, где одна звучит выше другой. Когда звук в тритоне переходит с одной ноты на другую (например, соль-диез между двумя до), можно совершенно обоснованно интерпретировать ноту как более высокую или более низкую, чем предыдущая.
Другое парадоксальное свойство тритонов — это ощущение, что звук постоянно становится ниже, хотя высота звука не меняется. На нашем видео вы можете наблюдать эффект в течение целых десяти минут.
Парадокс Банаха-Тарского
Представьте себе, что вы держите в руках шар. А теперь представьте, что вы начали рвать этот шар на куски, причём куски могут быть любой формы, какая вам нравится. После сложите кусочки вместе таким образом, чтобы у вас получилось два шара вместо одного. Каков будет размер этих шаров по сравнению с шаром-оригиналом?
Согласно теории множеств, два получившихся шара будут такого же размера и формы, как шар-оригинал. Кроме того, если учесть, что шары при этом имеют разный объём, то любой из шаров может быть преобразован в соответствии с другим. Это позволяет сделать вывод, что горошину можно разделить на шары размером с Солнце.
Хитрость парадокса заключается в том, что вы можете разорвать шары на куски любой формы. На практике сделать это невозможно — структура материала и в конечном итоге размер атомов накладывают некоторые ограничения.
Для того чтобы было действительно возможно разорвать шар так, как вам нравится, он должен содержать бесконечное число доступных нульмерных точек. Тогда шар из таких точек будет бесконечно плотным, и когда вы разорвёте его, формы кусков могут получиться настолько сложными, что не будут иметь определенного объёма. И вы можете собрать эти куски, каждый из которых содержит бесконечное число точек, в новый шар любого размера. Новый шар будет по-прежнему состоять из бесконечных точек, и оба шара будут одинаково бесконечно плотными.
Если вы попробуете воплотить идею на практике, то ничего не получится. Зато всё замечательно получается при работе с математическими сферами — безгранично делимыми числовыми множествами в трехмерном пространстве. Решённый парадокс называется теоремой Банаха-Тарского и играет огромную роль в математической теории множеств.
Парадокс совпадения дней рождения
Суть философского и математического вопроса вот в чем: если собрать в одном месте 23 и более человек, то вероятность совпадения дней рождения у двух из них превысит 50 %. В группе, насчитывающей от 60 участников, этот шанс повышается до 99 %, а вот полное совпадение возможно только в том случае, если вместе собрались не меньше 367 человек.
Математически этот парадокс обосновал немец Петер Густав Дирихле. Научно парадокс никак не входит в противоречие с логикой, зато отлично доказывает, как отличается интуитивный подход от математического – на первый взгляд может показаться, что для сравнительно небольшой первой группы вероятность совпадения дней рождения кажется необоснованно завышенной.
Что было раньше – курица или яйцо?
Этим вопросом наверняка хотя бы раз в жизни задавался любой из нас. Что же появилось на свет раньше – несушка или яйцо? Последователи теории эволюции убеждены в том, что птицы появились из яиц куда раньше, чем отряд куриных. Поэтому очевидно, что яйцо было раньше. Но и замена “курицы” на просто “птицу” в парадоксе тоже довольно легко приводит к тому же самому ответу – динозавры тоже размножались яйцами, а они возникли еще раньше птиц.
Если учесть все эти нюансы, парадокс должен быть сформулирован так: что появилось раньше – первое живое существо, которое откладывало яйца, или яйцо, из которого это существо и появилось? На этом этапе вопрос становится объективно неразрешимым, поскольку любой из ответов предполагает известное число оговорок и допущений.
Животные в процессе эволюции проходили через бесконечное число трансформаций: это касалось и способа выведения потомства. На некоторых из стадий развития они откладывали то, что можно условно назвать “пра-яйцами”, но с сегодняшней точки зрения определить эти предметы как настоящие яйца все же нельзя.
Парадокс экологического баланса
Модель «хищник-жертва» — это уравнение, описывающее реальную экологическую обстановку. Например, модель может определить, насколько изменится численность лис и кроликов в лесу. Допустим, что травы, которой питаются кролики, в лесу становится всё больше. Можно предположить, что для кроликов такой исход благоприятен, потому что при обилии травы они будут хорошо размножаться и увеличивать численность.
Парадокс экологического баланса утверждает, что это не так: сначала численность кроликов действительно возрастёт, но рост популяции кроликов в закрытой среде (лесу) приведёт к росту популяции лисиц. Затем численность хищников увеличится настолько, что они уничтожат сначала всю добычу, а потом вымрут сами.
На практике этот парадокс не действует на большинство видов животных — хотя бы потому, что они не живут в закрытой среде, поэтому популяции животных стабильны. Кроме того, животные способны эволюционировать: например, в новых условиях у добычи появятся новые защитные механизмы.
Парадокс половины пути
Чтобы пройти любой путь, нужно сперва преодолеть его половину: для этого нужно покрыть шагами половину половины, а до того – половину половины той половины. Продолжать можно без конца. Стало быть, движение становится невозможно в принципе. Этот парадокс служит доказательством статичности Вселенной – именно так предполагал Парменид. Человечество всегда отторгало эту загадку, хотя бы потому, что каждый из миллиардов людей отлично понимал, что движется и он сам, и все, что находится вокруг него.
В XIX веке было предложено математическое решение парадокса: если принять число всего пути за единицу, то она должна получиться путем сложения всех его частей – от ½ и ¼ и далее до самых малых дробей. Она и получается, если сложить все части вместе – если, конечно, не принимать в расчет, что 0,999999999 все же не совсем единица.
Закон Бенфорда
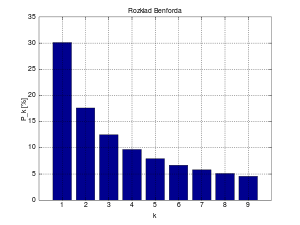Каков шанс, что случайное число начнётся с цифры «1»? Или с цифры «3»? Или с «7»? Если вы немного знакомы с теорией вероятности, то можете предположить, что вероятность — один к девяти, или около 11%.
Если же вы посмотрите на реальные цифры, то заметите, что «9» встречается гораздо реже, чем в 11% случаев. Также куда меньше цифр, чем ожидалось, начинается с «8», зато колоссальные 30% чисел начинаются с цифры «1». Эта парадоксальная картина проявляется во всевозможных реальных случаях, от количества населения до цен на акции и длины рек.
Физик Фрэнк Бенфорд впервые отметил это явление в 1938-м году. Он обнаружил, что частота появления цифры в качестве первой падает по мере того, как цифра увеличивается от одного до девяти. То есть «1» появляется в качестве первой цифры примерно в 30,1% случаев, «2» появляется около 17,6% случаев, «3» — примерно в 12,5%, и так далее до «9», выступающей в качестве первой цифры всего лишь в 4,6% случаев.
Чтобы понять это, представьте себе, что вы последовательно нумеруете лотерейные билеты. Когда вы пронумеровали билеты от одного до девяти, шанс любой цифры стать первой составляет 11,1%. Когда вы добавляете билет № 10, шанс случайного числа начаться с «1» возрастает до 18,2%. Вы добавляете билеты с № 11 по № 19, и шанс того, что номер билета начнётся с «1», продолжает расти, достигая максимума в 58%. Теперь вы добавляете билет № 20 и продолжаете нумеровать билеты. Шанс того, что число начнётся с «2», растёт, а вероятность того, что оно начнётся с «1», медленно падает.
Закон Бенфорда не распространяется на все случаи распределения чисел. Например, наборы чисел, диапазон которых ограничен (человеческий рост или вес), под закон не попадают. Он также не работает с множествами, которые имеют только один или два порядка.
Тем не менее, закон распространяется на многие типы данных. В результате власти могут использовать закон для выявления фактов мошенничества: когда предоставленная информация не следует закону Бенфорда, власти могут сделать вывод, что кто-то сфабриковал данные.
Парадокс неподвижности стрелы
Выпущенную из лука стрелу следует признать неподвижной, поскольку в каждый момент времени она находится в состоянии покоя. А раз она покоится постоянно, то она неподвижна всегда. Но стрела летит – и, следовательно, подвижна.
Проблема заключается в том, что в каждый момент времени ничего не происходит вообще, потому что проходит всего ноль секунд – а значит, и движения никакого нет и быть не может. Время в целом состоит из вот таких нулевых мгновений, и если ни в какое из них ничего не происходит, значит, ничего никогда происходить и двигаться не должно.
От сумасшествия при размышлениях об этом парадоксе спасает теория относительности. Объект в движении отличается от объекта, который находится в состоянии покоя, – следовательно, они движутся с разными скоростями и по-разному воспринимаются сторонним наблюдателем.
Парадокс Моравека
При решении проблем, требующих вдумчивого рассуждения, у людей случаются затруднения. С другой стороны, основные моторные и сенсорные функции вроде ходьбы не вызывают никаких затруднений вообще.
Но если говорить о компьютерах, всё наоборот: компьютерам очень легко решать сложнейшие логические задачи вроде разработки шахматной стратегии, но куда сложнее запрограммировать компьютер так, чтобы он смог ходить или воспроизводить человеческую речь. Это различие между естественным и искусственным интеллектом известно как парадокс Моравека.
Ханс Моравек, научный сотрудник факультета робототехники Университета Карнеги-Меллона, объясняет это наблюдение через идею реверсного инжиниринга нашего собственного мозга. Реверсный инжиниринг труднее всего провести при задачах, которые люди выполняют бессознательно, например, двигательных функциях.
Поскольку абстрактное мышление стало частью человеческого поведения меньше 100 000 лет назад, наша способность решать абстрактные задачи является сознательной. Таким образом, для нас намного легче создать технологию, которая эмулирует такое поведение. С другой стороны, такие действия, как ходьба или разговор, мы не осмысливаем, так что заставить искусственный интеллект делать то же самое нам сложнее.
Следующий анекдот
На протяжении столетий в первый день апреля шутники не упускают случая посмеяться над ближними. Чтобы, если розыгрыш удался, с восторгом прокричать: «С первым апреля!» Впрочем, если шутка не удалась — еще забавней! Почему покатываются от смеха те, кто разыгрывает, а вовсе не те, кому эта шутка предназначалась? Прав ли был Аристотель, полагавший, что из всех живых существ юмор присущ только человеку, и отчего далеко не все смеются, когда в эфире идет «Аншлаг»?
Угрызения совести
Юмористы — самые печальные люди на свете. Так утверждал мой коллега, ведущий раздела смеха в одном серьезном издании. Особенно он напирал на эту мысль, когда главный редактор, не щадя чувств творца по отношению к творениям, а в нашем случае — анекдотам с полосы, предшествующей кроссворду, утверждал: «А вот это, Вася, не смешно!» Как водится, первого апреля незадачливый остряк попытался «разбавить скучный раздел искрометной шуткой» по поводу… чувства прекрасного самого главреда. И наконец-то попал! Ухахатывались все, кроме адресата: тот просто побагровел от ярости. Чтобы не вдаваться в подробности дальнейшего развития событий, обратимся к древним. Они, кстати, относились к юмору с определенной долей недоверия.
«Это инструмент соблазна, оружие, которое может быть убийственным», — предостерегал Цицерон. Его предшественник Платон и вовсе осуждал «гримасу безобразия», недостойную свободных людей, поскольку, по его мнению, она предполагала потерю самоконтроля.
«Юмор — это подарок нашей природы, — утверждает психотерапевт Борис Новодержкин.— Понимать шутки — значит ладить с окружающими. Просто его социальные функции могут быть очень разными: с одной стороны, он помогает заводить союзников и сплачивает социальную группу, с другой — может выполнять довольно жестокую функцию, становясь средством отторжения чужаков. Будучи одним из самых парадоксальных явлений, на физиологическом уровне смех представляет собой диффузную разрядку. Смеху практически всегда предшествует напряжение».
«Страх быть осмеянным — одна из самых сильных фобий человека, — развивает мысль гештальт-психолог Денис Новиков, — ведь быть смешным — значит быть нелепым, то есть делать что-то не совсем адекватное с таким видом, будто это нормально.
Довольно часто у тех, кто становится объектом насмешек, нарушены механизмы самовосприятия, они бывают социально наивными или попросту не обладают опытом».
По мнению психологов, у тех, кто любит посмеяться над кем-то, обострено чувство страха и неуверенности в собственной адекватности. Ведь что-то смешное можно отыскать в каждом из нас, и, когда люди смеются над чужой неловкостью, они подсознательно проецируют на объект насмешек свои собственные переживания.
Как сделать из обезьяны человека
Экстравагантную теорию об участии смеха в происхождении человека разработал американский эволюционист Джеймс Э. Кэрон. В статье, опубликованной в The International Journal of Humor Research, он пишет, что именно смех сыграл адаптивную роль в эволюции: «Те индивиды из числа наших предков, которые умели изображать на лице улыбку или производить звуки, характеризуемые как смех, обладали адаптивным преимуществом: улыбка и смех увеличивают шансы человека на выживание».
Как не быть смешным?
На самом деле в глупой ситуации может оказаться каждый из нас. А чтобы стать «заговоренным» от грозного оружия осмеяния, психологи советуют научиться смеяться… над собой!
«Если человек выставил себя в дурацком свете, скажем неудачно пошутил, и сразу сообразил, как ситуацию обыграть, — это ему только в плюс, — говорит Борис Новодержкин. — Прием “Какую глупость я сказал” работает безотказно как в многомиллионной аудитории телезрителей, так и в узкой компании, где все свои. Любая шутка имеет под собой самоиронию. Вы только предполагаете, что вас оценят, но не вправе требовать этого от окружающих».
Человек, способный посмеяться над «святая святых» — самим собой, априори обладает устойчивой самооценкой, причем настолько, что может позволить себе не поддерживать иллюзию собственного величия…
-
Анекдоты про рваные штаны
-
Мем шутки про расизм
-
Крутые шутки для вк
-
Квн шутки про путина
- Шутка петросяна про сантехника
Эффект Мпембы
Перед вами два стакана воды, совершенно одинаковые во всём, кроме одного: температура воды в левом стакане выше, чем в правом. Поместите оба стакана в морозилку. В каком стакане вода замёрзнет быстрее? Можно решить, что в правом, в котором вода изначально была холоднее, однако горячая вода замёрзнет быстрее, чем вода комнатной температуры.
Этот странный эффект назван в честь студента из Танзании, который наблюдал его в 1986-м году, когда замораживал молоко, чтобы сделать мороженое. Некоторые из величайших мыслителей — Аристотель, Фрэнсис Бэкон и Рене Декарт — и ранее отмечали это явление, но не были в состоянии объяснить его. Аристотель, например, выдвигал гипотезу, что какое-либо качество усиливается в среде, противоположной этому качеству.
Эффект Мпембы возможен благодаря нескольким факторам. Воды в стакане с горячей водой может быть меньше, так как часть её испарится, и в результате замёрзнуть должно меньшее количество воды. Также горячая вода содержит меньше газа, а значит, в такой воде легче возникнут конвекционные потоки, следовательно, замерзать ей будет проще.
Другая теория строится на том, что ослабевают химические связи, удерживающие молекулы воды вместе. Молекула воды состоит из двух атомов водорода, связанных с одним атомом кислорода. Когда вода нагревается, молекулы немного отодвигаются друг от друга, связь между ними ослабевает, и молекулы теряют немного энергии — это позволяет горячей воде остывать быстрее, чем холодной.
Парадокс убитого в прошлом дедушки
Идея убить одного из своих предков, переместившись на машине времени в прошлое, пришла в голову фантаста Рене Баржавеля. Он описал этот случай в своей книге “Неосторожный путешественник”.
Что же случится, если кому-то удастся переместиться на несколько десятков лет назад и убить собственного дедушку еще до того, как он встретит бабушку? Если вы относите себя к врожденным гуманистам, можно не убивать славного парня, а просто попытаться другими способами препятствовать этой знаковой встрече, например посадить потенциального дедушку в отрезанный от всего мира дом или увезти его за тридевять земель. Но сам по себе парадокс никуда от этого не денется.
Возможно, дедушка влюбится в какую-то другую женщину – и тогда у родителей путешественника может быть другой цвет глаз или телосложение. Если же он проведет дни своей жизни в одиночестве, то кто-то из родителей путешественника не появится на свет, соответственно, и он сам тоже не родится. Но в этом случае некому будет отправиться в прошлое, чтобы помешать дедушке осуществить свои матримониальные желания. Парадокс, да и только.
Именно этот случай приводится в качестве аргумента принципиальной невозможности путешествий во времени, но некоторые из спорщиков сходятся во мнении о существовании бесконечного множества альтернативных версий реальности – в одной из них путешественник действительно никогда не рождается, а дедушка в разных из них умирает десятками различных способов и женится на разных женщинах.